The Dot Product Calculator is an essential tool for anyone working with vectors, whether you’re in physics, engineering, computer science, or mathematics. By simplifying complex vector calculations, it helps you understand how two vectors interact. If you’re dealing with large datasets or solving physics problems, using this calculator will save you time and effort, allowing you to focus on interpreting the results rather than getting lost in the math.
In this guide, we’ll explore how the Dot Product Calculator works, why it’s important, and how it pairs with the Endpoint Calculator to provide complete vector solutions. By the end, you’ll have a clear understanding of how these tools can improve your mathematical efficiency and accuracy.
What is a Dot Product?
Before diving into the Dot Product Calculator, let’s briefly explain what a dot product is. The dot product, also known as the scalar product, is a mathematical operation that multiplies two vectors and returns a scalar, or a single number. It’s widely used in various fields like physics to calculate work done by a force, or in computer science for determining vector similarity.
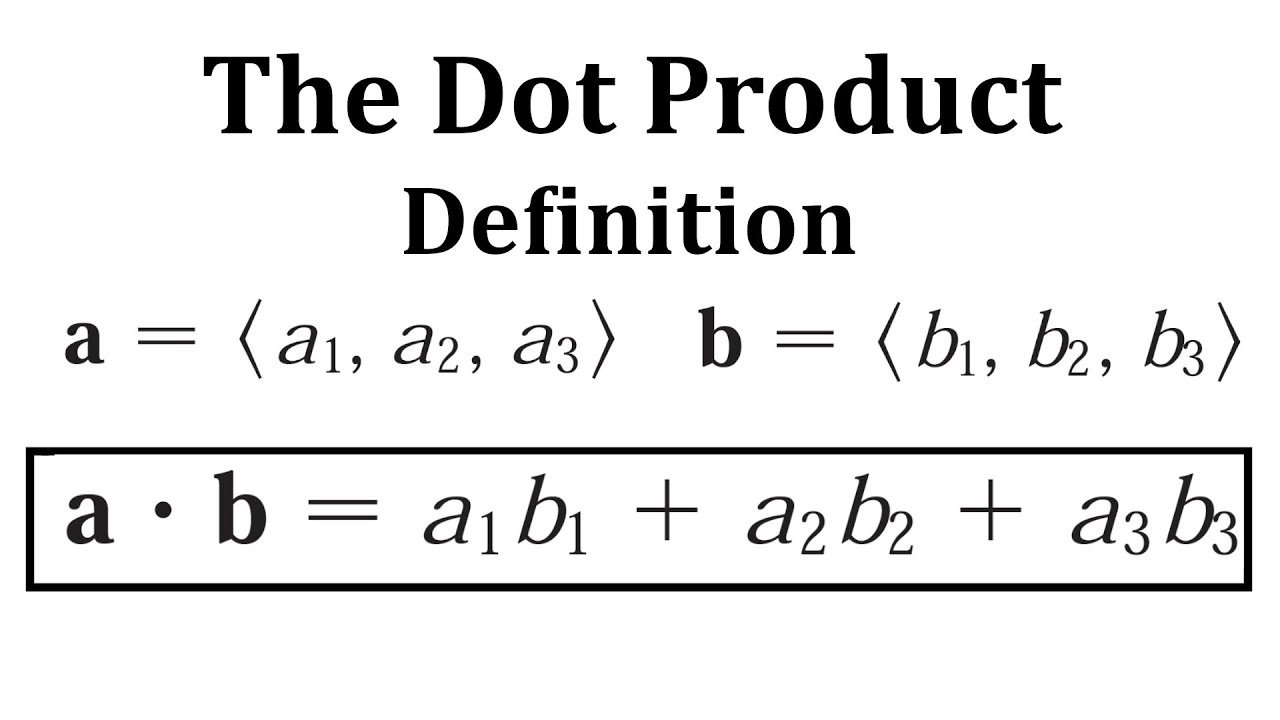
The formula for calculating the dot product of two vectors A and B is as follows:
A · B = A₁B₁ + A₂B₂ + A₃B₃
Where:
- A₁, A₂, A₃ are the components of vector A
- B₁, B₂, B₃ are the components of vector B
This result helps you determine how aligned two vectors are. A large, positive result indicates they are in the same direction, while a result close to zero suggests the vectors are perpendicular. Negative results mean the vectors point in opposite directions.
Why Use the Dot Product Calculator?
Manually calculating dot products can be a tedious and error-prone process, especially when working with larger vectors. The Dot Product Calculator simplifies this task, offering several key advantages:
- Accuracy: With manual calculations, it’s easy to make small mistakes that lead to incorrect results. The calculator eliminates this risk by providing accurate outputs instantly.
- Efficiency: Solving dot products by hand can be time-consuming. The calculator provides results in seconds, enabling you to focus on analysis rather than calculations.
- User-Friendly: The tool is easy to use, even for those who may not have a strong mathematical background. Whether you’re solving 2D or 3D vector problems, the calculator can handle both.
How to Use the Dot Product Calculator
Using the Dot Product Calculator is simple and intuitive. Follow these steps:
- Input the Components of Vector A: Enter the values for A₁, A₂, and A₃ for a 3D vector, or A₁ and A₂ for a 2D vector.
- Input the Components of Vector B: Similarly, input the values for B₁, B₂, and B₃ (or B₁ and B₂ for 2D vectors).
- Calculate: Click the “Calculate” button, and the tool will instantly provide the dot product of the two vectors.
For example, if we have the following vectors:
A = (3, -2, 5)
B = (4, 0, -1)
The dot product calculation will be:
A · B = (3 × 4) + (-2 × 0) + (5 × -1) = 12 + 0 – 5 = 7
The calculator provides the result immediately, saving you time and effort.
Applications of the Dot Product in Real Life
The Dot Product Calculator is especially useful in a variety of fields. Here are some practical applications:
- Physics: The dot product is often used to calculate the work done by a force. Work is the dot product of the force vector and the displacement vector. For example, if you apply a force over a certain distance, the dot product can tell you how much of that force is effectively contributing to the movement.
- Engineering: Engineers use dot products to analyze the forces acting on structures. By calculating the dot product, they can determine how much force is applied in a specific direction, which is crucial for ensuring structural integrity.
- Computer Graphics: In 3D rendering, the dot product is used to determine the lighting on a surface. The angle between the light source and the surface normal is calculated using the dot product, allowing for realistic shading and lighting effects in computer graphics.
- Data Science and Machine Learning: The dot product is used to measure the similarity between vectors. For instance, in machine learning, the dot product can be used to evaluate the similarity between feature vectors, helping in the classification of data.
The Role of the Endpoint Calculator
The Endpoint Calculator is another useful tool in vector math. While the Dot Product Calculator helps you understand the relationship between two vectors, the Endpoint Calculator helps you find the final coordinates of a vector after it has been extended from a starting point by a certain distance in a given direction.
For example, if you’re calculating how far an object has moved under a specific force, the Endpoint Calculator can determine its final position. These two calculators are often used together to solve complex vector problems.
How to Use the Endpoint Calculator
Using the Endpoint Calculator is just as straightforward as using the Dot Product Calculator:
- Enter the Starting Point Coordinates: Input the x, y, and z coordinates of the starting point (for 3D vectors) or just x and y for 2D vectors.
- Enter the Vector’s Direction and Magnitude: Input how far the vector moves along each axis (Δx, Δy, Δz).
- Calculate the Endpoint: The calculator will return the final coordinates of the vector’s endpoint.
For example, if a force moves an object from the point (1, 2, 3) by a vector of (4, -1, 2), the calculator will show that the endpoint is:
(1 + 4, 2 – 1, 3 + 2) = (5, 1, 5)
This makes it easy to visualize the movement and understand the effects of vector forces in a 3D space.
The Importance of Combining Dot Product and Endpoint Calculators
When solving vector problems, using both the Dot Product Calculator and the Endpoint Calculator gives you a more complete understanding. For example, in physics, you may need to determine both the work done by a force (dot product) and where the object ends up after the force has been applied (endpoint). These calculators simplify these tasks and ensure accuracy.
Practical Example: Work Done by a Force
Let’s say you’re asked to calculate the work done by a force of (6, 2, -1) moving an object by a displacement of (4, -3, 5). First, you would use the Dot Product Calculator:
Force = (6, 2, -1)
Displacement = (4, -3, 5)
The dot product would be:
Work = (6 × 4) + (2 × -3) + (-1 × 5) = 24 – 6 – 5 = 13
The total work done is 13 units. If you wanted to know where the object ends up after the displacement, you would use the Endpoint Calculator to find the final position based on the initial position and movement.
Benefits of the Dot Product Calculator
- Faster Calculations: By using the Dot Product Calculator, you save time on manual computations and focus more on interpreting your results.
- Accuracy: Ensures that you get the correct results without worrying about calculation mistakes.
- Wide Applications: From physics and engineering to computer science, the calculator is invaluable for vector-related problems.
Call to Action
Ready to simplify your vector calculations? Head over to The Mathematics Master and start using the Dot Product Calculator and Endpoint Calculator today. Whether you’re a student, engineer, or data scientist, these tools will help you master vector math with ease and precision.
Conclusion
The Dot Product Calculator is an indispensable tool for anyone working with vectors. It helps you calculate how two vectors interact and streamlines complex calculations, making it ideal for physics, engineering, and other technical fields. Paired with the Endpoint Calculator, you have a complete solution for solving vector-related problems.
Visit The Mathematics Master and make vector math simple and accurate!