Dot product calculator has revolutionized the way we approach vector operations in mathematics, physics, and various other fields. These powerful tools simplify complex calculations, making them indispensable for students, professionals, and researchers alike. In this comprehensive guide, we’ll explore the ins and outs of dot product calculators, their applications, and how they can enhance your understanding of linear algebra and beyond.
What is a Dot Product Calculator?
A dot product calculator is a specialized tool designed to compute the scalar product of two vectors. This fundamental operation in linear algebra involves multiplying corresponding components of two vectors and then summing the results. While the concept might sound simple, the calculations can become complex and time-consuming, especially when dealing with higher-dimensional vectors.
The Basics of Calculating Dot Products
Before diving into the calculator’s specifics, let’s review the basic concept of dot products:
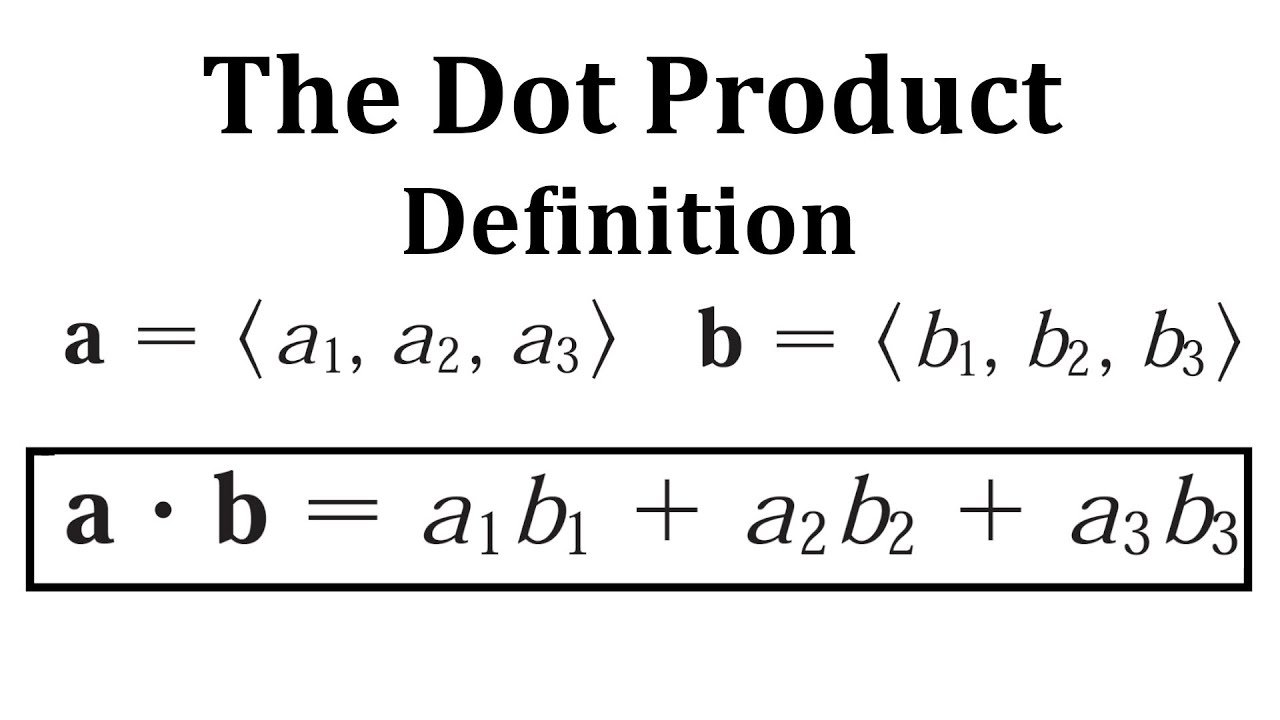
For two vectors A = (a1, a2, a3) and B = (b1, b2, b3), their dot product is calculated as:
A · B = a1b1 + a2b2 + a3b3
This operation results in a scalar value, which provides valuable information about the relationship between the two vectors.
The Importance of Dot Product Calculators
Dot product calculators streamline this process, allowing users to input vector components and receive instant, accurate results. This efficiency is crucial in various scenarios:
- Educational Settings: Students can verify their manual calculations and gain a deeper understanding of vector operations.
- Research Applications: Scientists and engineers can quickly perform complex vector analyses.
- Real-world Problem Solving: Professionals in fields like computer graphics, robotics, and physics can apply dot products to solve practical challenges.
How to Use a Dot Product Calculator
Using a dot product calculator is straightforward:
- Input the components of the first vector
- Enter the components of the second vector
- Click the “Calculate” button
- Review the result
Most calculators also provide step-by-step solutions, enhancing the learning experience.
Applications of Dot Product Calculators
The versatility of dot product calculators extends far beyond basic mathematics:
1. Physics and Mechanics
In physics, dot products are essential for calculating work done by a force:
Work = Force · Displacement
Dot product calculators simplify these calculations, making them invaluable in mechanical engineering and physics research.
2. Computer Graphics
3D rendering relies heavily on vector operations. Dot products are used to calculate:
- Light intensity in shading algorithms
- Collision detection between objects
- Camera orientations in virtual environments
3. Machine Learning and Data Science
In machine learning, dot products are fundamental to many algorithms:
- Calculating similarity measures between data points
- Implementing neural network layers
- Performing feature extraction in high-dimensional spaces
4. Geometry and Trigonometry
Dot product calculators assist in:
- Finding angles between vectors
- Determining vector projections
- Calculating the orthogonality of vectors
Advanced Features of Dot Product Calculators
Modern dot product calculators often come with additional functionalities:
- Vector Normalization: Automatically normalize vectors before calculation.
- Multiple Vector Support: Calculate dot products for more than two vectors simultaneously.
- Visualization Tools: Graphically represent vectors and their dot products.
- Integration with Other Calculators: Seamlessly switch between vector operations like cross products and scalar multiplications.
The Mathematics Behind Dot Product Calculators
Understanding the underlying mathematics enhances appreciation for these tools:
- Algebraic Perspective: The dot product is an algebraic operation that maps two vectors to a scalar.
- Geometric Interpretation: The dot product relates to the angle between vectors: A · B = |A| |B| cos(θ) Where |A| and |B| are vector magnitudes, and θ is the angle between them.
- Matrix Multiplication: In linear algebra, dot products are equivalent to matrix multiplication of a row vector with a column vector.
Choosing the Right Dot Product Calculator
When selecting a dot product calculator, consider:
- Accuracy: Ensure the calculator provides precise results, especially for scientific applications.
- User Interface: Look for an intuitive design that facilitates easy input and clear output.
- Additional Features: Consider calculators that offer step-by-step solutions or graphing capabilities.
- Compatibility: Choose a calculator that works well on your preferred devices or platforms.
Enhancing Your Skills with Dot Product Calculators
To maximize the benefits of using a dot product calculator:
- Practice Regularly: Use the calculator alongside manual calculations to reinforce your understanding.
- Explore Real-world Applications: Apply dot products to practical problems in your field of study or work.
- Combine with Other Tools: Integrate dot product calculations with other mathematical operations for comprehensive problem-solving.
The Future of Dot Product Calculators
As technology advances, we can expect dot product calculators to evolve:
- AI Integration: Smarter calculators that can interpret natural language inputs and provide context-aware solutions.
- Augmented Reality: Visualize vector operations in 3D space using AR technology.
- Cloud-based Collaboration: Share and collaborate on vector calculations in real-time with peers or colleagues.
Conclusion
Dot product calculators are powerful tools that simplify complex vector operations, making them accessible to a wide range of users. From students grappling with linear algebra concepts to professionals solving intricate engineering problems, these calculators offer efficiency, accuracy, and insight.
By understanding how to use dot product calculators effectively, you can enhance your problem-solving skills and gain a deeper appreciation for the underlying mathematics. Whether you’re calculating work in physics, optimizing computer graphics, or exploring machine learning algorithms, mastering the use of dot product calculators will undoubtedly prove invaluable. Additionally, when combined with other tools like endpoints calculator, they form a comprehensive suite for vector analysis and geometric problem-solving.
Ready to explore the world of vector operations? Visit The Mathematics Master to access our state-of-the-art dot product calculator, endpoints calculator, and a wide range of other mathematical tools. Elevate your computational skills and unlock new possibilities in your mathematical journey today!
Read more blogs on this site.